自由飞翔的图案:伊斯兰工匠的高智商拼图游戏

女士们,先生们,老少爷们儿们!在下张大少。
1 形态构成
五重对称图案在阿拉伯世界的东部比在西方更常见,但图1中所示的图案随处可见。我们称它为“基本的”五重对称图案。一种流行的波斯风格图案的解释使用了由“原型拼块”(或“Girih拼块”,来自著名的《Topkapi卷轴》,见[9])构成的底层等角网络的概念。但是,如果一个图案来自这样的“原型拼块”,那么这个原型拼块从何而来?当然,如果原型拼块已经被使用,那么这不是故事的开始。当我们看到图8.1所示的使用特定波斯拼块组T1的图案背后的原始拼块时,我们不必感到惊讶,因为这是一个必然的结果。也就是说,我们遇到一个老问题:先有鸡还是先有蛋。
令人惊叹的是所有这些图案之间的高度联系,以及各种可能的绘制方法。
图1:前奏,“基本图案”,源自10个五边形。它也可以被看作是由装饰过的彭罗斯菱形组成的(右边部分)。
现在,让我们来看看来自Karatay的这个著名图案(图2):

图2:来自Karatay的图案的一个视角。J.Rigby[10]已经从另一个角度研究过这个图案。
首先,去掉线条的宽度(2.2),然后只考虑图案的四分之一部分(2.3)。现在,我们要再做两个简化(2.4,2.5):去掉大星星里面的拼块,用更简单的拼块取代两个对角的十角星。我们现在可以把最初的Karatay图案看作只是这个基本图案的一个变体。
现在,在这一点上,我们可以注意到,有一个彭罗斯的小菱形在长方形(2.6)内完全匹配。难道我们不能说,整个图案是一个更大的图案的一部分,由装饰过的彭罗斯菱形组成?
因此我们产生了形态构成的想法:我们设计一系列装饰的小彭罗斯菱形,从最简单的(较小的)到更复杂的。对于每种解决方案,我们都必须设计相关的大菱形(如果可能的话)。对于复杂度步骤n,一对[VnS(小菱形),VnL(大菱形)]不仅定义一个图案,而且定义一个族Vn,因为菱形可以以不同的排列(周期性或非周期性,见图3)放在一起,并且因为可能的局部变化。
拼块的规则:线条的连续性,所有角度都是36°的倍数。
在这个系统中,上面的图案属于V4系列(图3)。
有趣的是,来自Maghara的著名图案也属于同一系列(图5)!

图3:形态构成。左下角是“五角星”的可能装饰,D。
我们称“五角星”为我们的初始的星星(D)。它的中心是36°扇形的顶部。请注意,它可以旋转18°,从而产生一个其他的系列,在这篇文章中暂不论述……
在第二步,我们有两个解决方案,V2L和V2L1用于大菱形。因此,有两个图案系列,V2由V2S和V2L组成,V2.1由V2S和V2L1组成。
当然,当边上的图案对称的时候,把菱形摆在一起就比较容易。
但是,V0呢?稍后再谈(图7)……
图4:结构。1-4需要对称的边缘。1-6是周期性或径向的。7-8:走向非周期性。
应用1,来自V4系列:对两个著名的传统图案的分析

图5:V4图案。
图5:V4图案。矩形窗内(A)是Karatay图案的结构(1/4嵌板,更多内容见图2),也是Maragha图案的结构。底部:从另一个角度看,Maragha图案可以被认为是来自一个装饰过的基本图案(见第8.4节)。
应用2,来自V0系列:“X-拼图”

图6
图6:这个拼图是由两个彭罗斯菱形图组成的,上面装饰着两条X形线,XL和XS,来自V0(图3)。左下角:不合适的配置(线条被打断)。因为每个角度都是36°的倍数,我们注意到1代表36°,3代表72°,等等。灰色图案是由X线画出的完整的拼块集。当X拼块拼在一起时,让“X-图案”成为X线所画的图案。
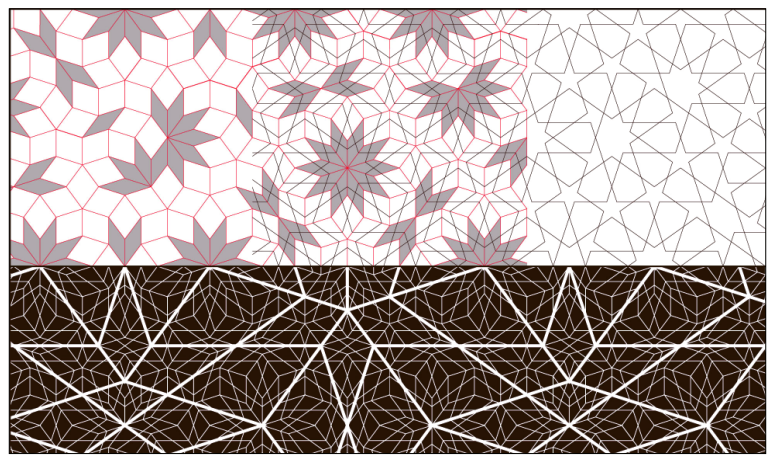
图7
图7 上图:彭罗斯图案和X图案拓扑对偶。下图:自相似特性在紧缩过程中的应用。
2 拼块,原型拼块,“元图案”
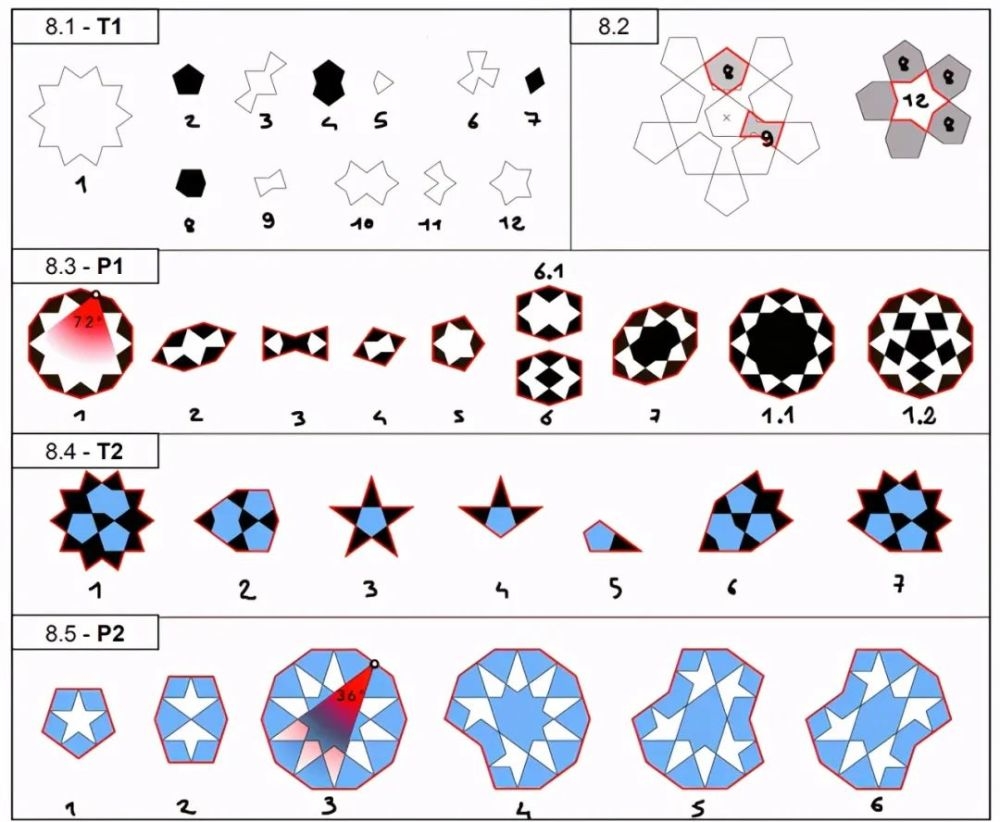
图8
图8 1: 一组波斯风格的拼块,T1;
2:拼块8,9,12的来源;
3:相关的原型拼块集P1(编号7,来自Cromwell,在本文中没有使用);
4:“元拼块”T2,由T1的拼块装饰;
5:相关的原型拼块集P2(在大多数情况下,我们只需要1-4号)。
“原型拼块”(或“Girih拼块”,见[4],[6])是装饰的多边形,构成一个等距的底层网络。从多边形的每条边的中间点引出的线在P1中成72°角,在P2中成36°角。任何由集合T1构成的图案都可以被看作是由原型拼块构成的(这里没有足够的空间来演示)。
图9
图9:使用拼块1、6、8、12的图案示例,来自V2L1的变体(图3),以及相关的原始拼块网络P1。如果我们用P2代替P1,我们得到的是基本图案(图1)。如果我们应用汉金的多边形接触技术,也会得到同样的图案(见[5])。
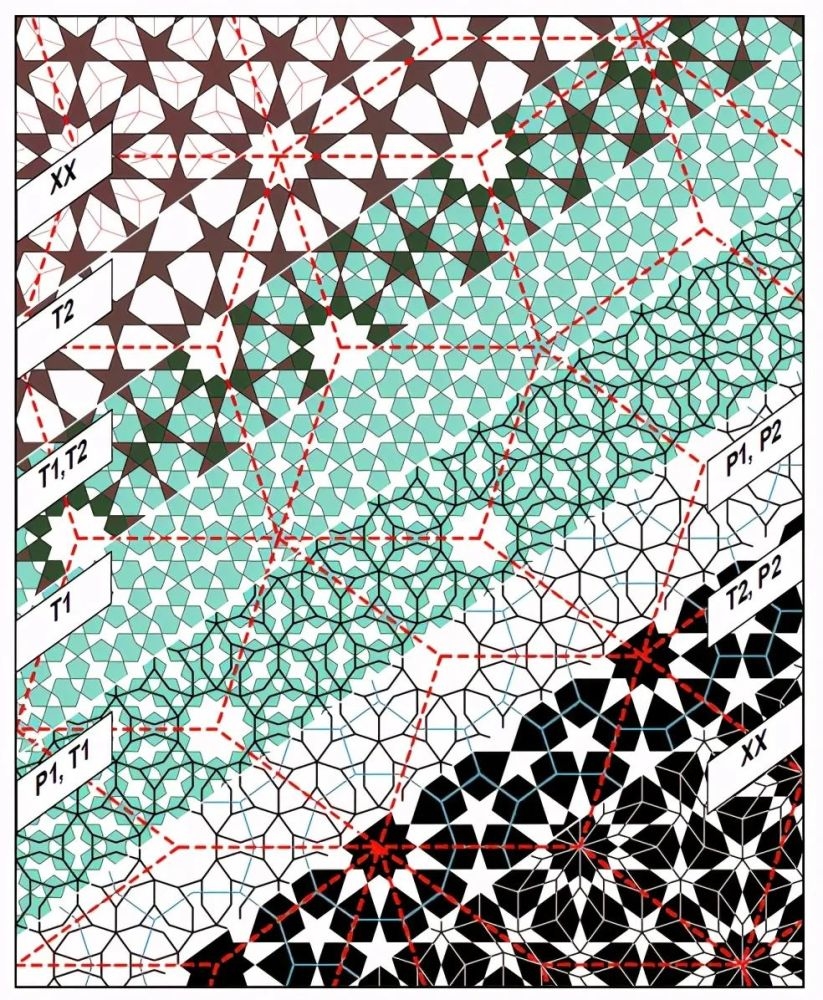
图10
图10:波斯图案T1、基本图案T2、原型拼块P1和P2、X拼图XX和彭罗斯菱形结构(虚线)的变化和关系。并非完全详尽。

图11:这些概念的应用
结论
人类的头脑渴望一个简单的、包罗万象的解释。希望这个世界比任何一种理论都更加丰富和复杂。关于这些图案,我在这里试图说明它们不能被一个解释或观点所涵盖。他们穿越不同的理论、风格、国家和时代。安达卢西语,阿拉伯语,波斯语,这些图案不关心边界:它们自由飞翔,汪洋恣肆。
参考文献
[1] Jay Bonner, Three traditions of self-similarity in fourteenth and fifteenth century Islamic geometric ornament, Meeting Alhambra, Proc. ISAMA-Bridges, pp.1-12, 2003.
[2] J.Bourgoin, LesEléments de l’ArtArabe, Firmin-Didot,1879. Plates reprinted in Arabic Geometric Pattern and Design, Dover Publications,1973.
[3] J.M. Castera. Arabesques, Paris, ACR, 1996. English version, 1999.
[4] Peter R. Cromwell, The Search for Quasi-periodicity in Islamic 5-fold Ornament, Math. Intelligencer 31 no 1, pp36-56, 2009.
[5] C.S.Kaplan, Islamic star patterns from polygons in contact, Graphics Interface, ACM International Conference Proceeding Series 112, pp.177-186, 2005.
[6] P.J. Lu and P.J. Steinhardt, Decagonal and quasi-crystalline tilings in medieval Islamic architecture, Science 315, pp. 1106-1110, 2007.
[7] E.Makovicky, 800-year old pentagonal tiling fromMaragha, Iran, and the new varieties of aperiodic tiling it inspired, Fivefold Symmetry, ed. I. Hargittai, World Scientififi c, pp.67-86, 1992.
[8] E.Makovicky, Another look at the Blue Tomb of Maragha, a site of the first quasicrystaline Islamic pattern, Symmetry: Culture and Science Vol. 19, Numbers 2-3, pp. 127-151, 2008.
[9] G.Necipogglu, The TopkapiScroll : Geometry and Ornament in Islamic Architecture, GettyCenter Publication,1995.
[10] J.Rigby, A Turkish interlacing pattern and the golden ratio, Mathematics in School, Vol. 34 N°.1, pp. 16-24, 2005.
[11] Jean-Marc Castera,Flying Patterns
最后照例放几本扯犊子书目
青山不改,绿水长流,在下告退。



